हेल्लो दोस्तों, आपका हमारी इस नई पोस्ट मैं स्वागत है। पिछली पोस्ट में हमने Quick Sort के बारे में पढ़ा था जो बहुत तेज़ है। लेकिन आज हम जिस एल्गोरिदम की बात करने जा रहे हैं, वह अपनी Stability और Consistency के लिए जाना जाता है। जी हाँ, आज का टॉपिक है Merge Sort।
इस पोस्ट में हमने आपको मर्ज सॉर्ट क्या है? (What is Merge Sort in Hindi?), यह Divide and Conquer तकनीक पर कैसे काम करता है? और यह बड़े डाटासेट्स (Large Datasets) के लिए इतना उपयोगी क्यों है, इसके बारे मैं विस्तार से बताया है।
अगर आप यह समझना चाहते हैं कि कंप्यूटर लाखों करोड़ों डाटा को बिना गलती किये कैसे सॉर्ट करता है, तो मर्ज सॉर्ट को समझना बहुत जरूरी है।
What is Merge Sort in Hindi? – मर्ज सॉर्ट क्या है?
Merge Sort एक बहुत ही powerful सोर्टिंग एल्गोरिदम है जो Divide and Conquer (बांटो और जीतो) के सिद्धांत पर काम करता है।
इसका लॉजिक बहुत सिंपल है:
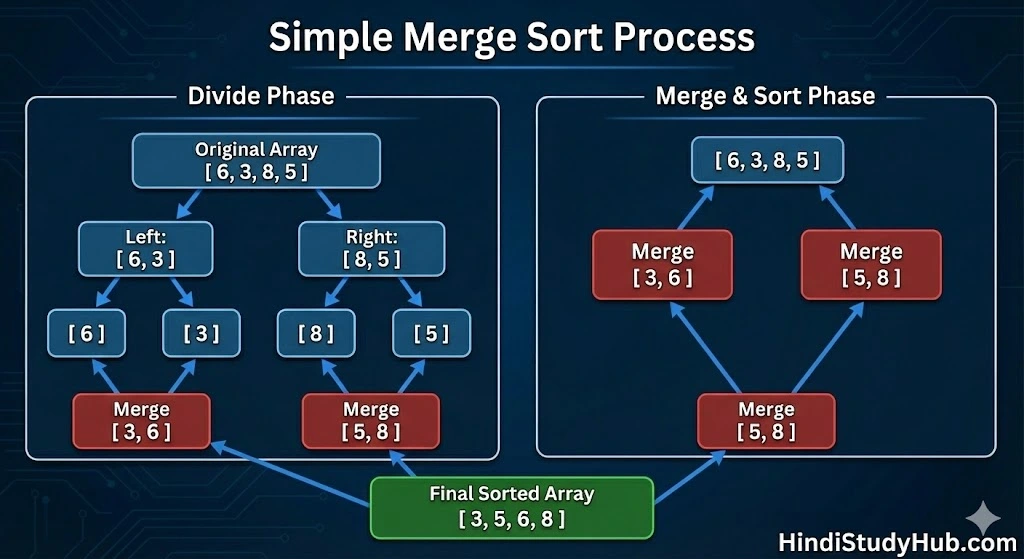
- Divide (बांटो): यह पहले पूरी लिस्ट को दो बराबर हिस्सों (halves) में तोड़ता है।
- Conquer (जीतो): फिर उन टूटे हुए हिस्सों को और छोटे हिस्सों में तोड़ता जाता है जब तक कि हर हिस्से में सिर्फ एक element न रह जाए।
- Merge (जोड़ो): अंत में, यह उन छोटे हिस्सों को वापस जोड़ता (Merge) है, लेकिन जोड़ते समय उन्हें Sort कर देता है।
Real Life Example: मान लीजिये आपके पास रद्दी कागज़ों का एक बड़ा ढेर है। आप पहले उसे आधा करके अपने दोस्त को देते हैं, फिर वो उसे आधा करता है। अंत में जब आप दोनों कागज़ों को वापस एक गड्डी में रखते हैं, तो आप उन्हें सही नंबर (Date या Page No) के हिसाब से जमाते हुए रखते हैं। यही मर्ज सॉर्ट है।
How Merge Sort Works in Hindi? – मर्ज सॉर्ट कैसे काम करता है?
मर्ज सॉर्ट मुख्य रूप से दो प्रक्रियाओं (processes) पर टिका है:
- Breaking Phase (तोड़ने का काम): एल्गोरिदम
Mid(मध्य बिंदु) निकालता है और array को तब तक बांटता रहता है जब तक कि हमारे पास single elements न बच जाएं। (क्योंकि एक अकेला element हमेशा sorted माना जाता है)। - Merging Phase (जोड़ने का काम): यह सबसे महत्वपूर्ण हिस्सा है। इसमें हम दो sorted sub-arrays को लेते हैं और उन्हें compare करके एक नई sorted array बनाते हैं।
- Sub-array 1:
[2, 5] - Sub-array 2:
[1, 4] - Merged Result:
[1, 2, 4, 5]
- Sub-array 1:
Step-by-Step Example of Merge Sort
चलिए एक उदाहरण देखते हैं। Array: [38, 27, 43, 10]
Step 1: Divide (बांटना)
- पूरी array को दो भागों में बांटा:
[38, 27]और[43, 10] - फिर इनको और बांटा:
[38],[27],[43],[10](अब हर element अकेला है)
Step 2: Merge & Sort (जोड़ना और सॉर्ट करना)
- अब
[38]और[27]को compare करके merge किया -> Result: [27, 38] - उधर
[43]और[10]को compare करके merge किया -> Result: [10, 43]
Step 3: Final Merge
- अब हमारे पास दो sorted lists हैं:
[27, 38]और[10, 43] - इन दोनों को compare करके merge करेंगे:
- 10 सबसे छोटा है ->
[10] - फिर 27 ->
[10, 27] - फिर 38 ->
[10, 27, 38] - फिर 43 ->
[10, 27, 38, 43]
- 10 सबसे छोटा है ->
Final Sorted Array: [10, 27, 38, 43]
Time Complexity Analysis – यह कितना कुशल है?
मर्ज सॉर्ट की सबसे बड़ी खासियत इसकी Consistency है। चाहे डाटा कैसा भी हो, यह हमेशा एक बराबर समय लेता है।
- Best Case: $O(n \log n)$
- Average Case: $O(n \log n)$
- Worst Case: $O(n \log n)$ (Quick Sort का Worst case $O(n^2)$ होता है, लेकिन Merge Sort यहाँ बाजी मार ले जाता है)
Space Complexity: $O(n)$
- यह इसका एक नुकसान (disadvantage) है। Merge Sort को काम करने के लिए अलग से मेमोरी (Auxiliary Space) की जरूरत पड़ती है, जो Quick Sort में नहीं पड़ती।
Merge Sort vs Quick Sort in Hindi – मर्ज सॉर्ट और क्विक सॉर्ट में से कौन बेहतर है?
| Feature | Merge Sort | Quick Sort |
| Speed | यह बड़े डाटा के लिए Consistent है। | यह छोटे डाटा के लिए Merge Sort से तेज है। |
| Space | इसमें ज्यादा मेमोरी लगती है ($O(n)$)। | इसमें कम मेमोरी लगती है ($O(1)$ or $O(\log n)$)। |
| Stability | यह Stable है (element का original order maintain रहता है)। | यह Unstable है। |
| Use Case | Linked List को sort करने के लिए यह सबसे बेस्ट है। | Arrays को sort करने के लिए यह सबसे बेस्ट है। |
Conclusion – निष्कर्ष
हमें उम्मीद है कि इस पोस्ट से आपने Merge Sort in Hindi (Divide and Conquer का जादू) अच्छी तरह समझ लिया होगा। संक्षेप में कहें तो, अगर आपके पास मेमोरी (RAM) की कोई कमी नहीं है और आप चाहते हैं कि सोर्टिंग का टाइम फिक्स रहे (Worst case में न फंसे), तो मर्ज सॉर्ट सबसे बेहतरीन विकल्प है।
अगर आपको यह लेख उपयोगी लगा हो तो इसे अपने कॉलेज ग्रुप्स में शेयर करें और कोडिंग करते रहें!
FAQs
Q1. Merge Sort का मुख्य नुकसान क्या है?
Ans: इसका मुख्य नुकसान Space Complexity है। इसे सोर्टिंग करने के लिए array के बराबर ही एक और temporary array की जरूरत पड़ती है।
Q2. क्या Merge Sort Recursive है?
Ans: हाँ, Merge Sort पूरी तरह से Recursion (रिकर्शन) पर आधारित है। यह खुद को बार-बार call करता है।
Q3. Linked List के लिए Merge Sort क्यों अच्छा है?
Ans: क्योंकि Linked List में nodes इधर-उधर बिखरे होते हैं और Merge Sort उन्हें बिना ज्यादा memory pointer change किये आसानी से sort कर सकता है।